What basic trigonometric identity would you use to verify that sin^2x +cos^2x/cos x = sec x

Question

asked Aug 28, 2020 180k views

2 Answers

Xiecs · Answer 1 · 2020-09-03T10:10:05+0000

Answer:

The basic identity used is
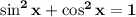$\bold{\sin ^(2) x+\cos ^(2) x=1}$ .

Solution:

In this problem some of the basic trigonometric identities are used to prove the given expression.

Let’s first take the LHS:

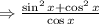
$\Rightarrow (\sin ^(2) x+\cos ^(2) x)/(\cos x)$

Step one:

The sum of squares of Sine and Cosine is 1 which is:

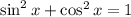
$\sin ^(2) x+\cos ^(2) x=1$

On substituting the above identity in the given expression, we get,

$\Rightarrow (\sin ^(2) x+\cos ^(2) x)/(\cos x)=(1)/(\cos x) \rightarrow(1)$

Step two:

The reciprocal of cosine is secant which is:

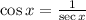
$\cos x=(1)/(\sec x)$

On substituting the above identity in equation (1), we get,

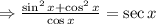
$\Rightarrow (\sin ^(2) x+\cos ^(2) x)/(\cos x)=\sec x$

Thus, RHS is obtained.

Using the identity
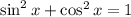$\sin ^(2) x+\cos ^(2) x=1$ , the given expression is verified.