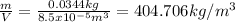Answer:
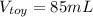
ρ=
Step-by-step explanation:
We know that density is equal to the mass divided of its volume
ρ
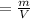
According to the Archimedes Principle the volume of displaced fluid is equivalent to the volume of the immersed object.
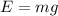
E=ρ
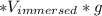
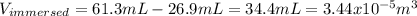
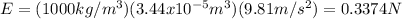
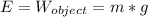
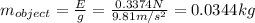
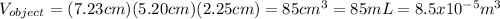
Now, we can calculate the density of the irregularly shaped object:
ρ=