Question

You want to buy a new sports coupe for $84,500, and the finance office at the dealership has quoted you an APR of 5.2 percent for a 60-month loan to buy the car. a. What will your monthly payments be? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.) b. What is the effective annual rate on this loan? (Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)

Answer 1

Ans. Your monthly payments will be $1,602.37 ; The effective annual rate is 5.33%

Step-by-step explanation:

Hi, first, we need to convert this APR rate into an effective monthly rate, that is, dividing 0.052/12 =0.00433 (or 0.4333%). Then we need to use the following equation and solve for A.

`PresentValue=(A((1+r)^(n)-1) )/(r(1+r)^(n) )`

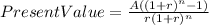
Where:

PresentValue= 84,500

A = periodic payments (the monthly payments that you need to make)

r = 0.004333333

n=60 months

So, let´s solve for A.

`84,500=(A((1+0.004333333)^(60)-1) )/(0.004333333(1+0.004333333)^(60) )`

`84,500=(0.296201791)/(0.005616874) A`

`84,500=A(52.73427328)`

`A= 1,602.37`

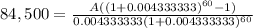
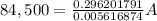
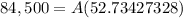
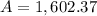
Now, in order to find the effective annual rate, we need to use the following equation.

`r(EffectiveAnnual)=((1+r(EffectiveMonthly))^(12) -1`

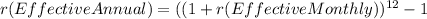
Notice that to find an effective rate you have to start with another effective rate, otherwise it won´t work. So everything should look like this.

`r(EffectiveAnnual)=((1+0.004333333))^(12) -1=0.0533`

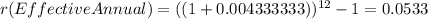
Meaning that the equivalent effective annual rate to 5.2% APR is 5.33% effective annual.

Best of luck.