Answer:
The valves perform above expectations.
Explanation:
We are given the following information in the question:
Population mean, μ = 7.6 pounds per square inch
Sample size, n = 140
Sample mean,
 = 7.8 pounds per square inch
= 7.8 pounds per square inch
Population standard deviation = 1.0 pounds per square inch
Level of significance = 0.05
We design the null and alternate hypothesis:
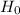 : μ = 7.6 pounds per square inch
: μ = 7.6 pounds per square inch
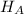 : μ > 7.6 pounds per square inch
: μ > 7.6 pounds per square inch
Formula:
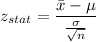
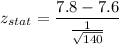

Now, we are performing a one tail test with level of significance of 0.05, we calculate the critical value of z with the help of standard normal distribution table.
Thus,
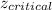 = 1.645
= 1.645
Result:
Since,

 is rejected.
is rejected.
Thus, we accept the alternate hypothesis.
Hence, the valve perform above expectations.