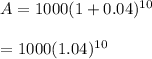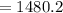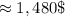Question

Select the correct answer.

What’s the future value of a $1,000 investment compounded at 8% semiannually for five years?

A : $1,469

B : $1,477

C : $1,480

D : $1,490

Answer 1

The future value of $1,000 invested at 8% compounded semiannually for five years is
`\bold{\$ 1,480}`

Solution:

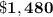
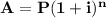`\bold{A = P (1 + i )^(n)}` ----------- equation 1

A = future value

P= principal amount

i = interest rate

n = number of times money is compounded

P = 1000

i = 8 %

`\mathrm{n} = \text { compounding period } * \text {number of years}`

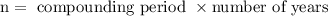
(Compounding period for semi annually = 2)

`\mathrm{n} = \text { compounding period } * \text {number of years}`

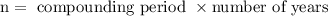
Dividing “i” by compounding period

`i = (8 \%)/(2) = 0.04`

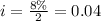
Solving for future value using equation 1

`\begin{array}{l}{A = 1000(1 + 0.04)^(10)} \\\\ {=1000 (1.04)^(10)}\end{array}`

`= 1480.2`

`\approx 1,480 \$`