Answer:
Sin F = 0.6
Explanation:
From triangle ABC, applying Pythagoras theorem to determine the length AB;
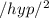 =
=
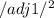 +
+
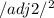
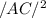 =
=
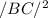 +
+
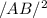
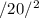 =
=
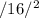 +
+
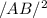
400 = 256 +
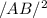
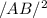 = 400 - 256
= 400 - 256
= 144
AB =
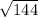
= 12
AB = 12, AC = 20, BC = 16
Therefore since ΔABC ≅ ΔDEF, and each side of triangle DEF is
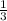 the length of the corresponding side of triangle ABC.
the length of the corresponding side of triangle ABC.
Then,
DE =
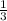 AB =
AB =
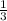 x 12
x 12
= 4
EF =
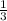 BC =
BC =
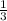 x 16
x 16
=
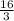
DF =
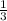 AC =
AC =
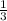 x 20
x 20
=
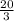
Then, applying trigonometric function to ΔDEF, we have;
Sin F =
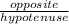
=
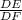
= 4 ÷
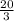
= 4 x
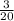
=

Sin F = 0.6