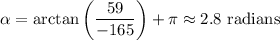Question

You are to make four straight-line moves over a flat desert floor, starting at the origin of an xy coordinate system and ending at the xy coordinates (-165 m, 59 m). The x component and y component of your moves are the following, respectively, in meters: (20 and 60), then (bx and -70), then (-20 and cy), then (-60 and -70). What are (a) component bx and (b) component cy? What are (c) the magnitude and (d) the angle (relative to the positive direction of the x axis) of the overall displacement?

Answer 1

(a) The sum of all the x displacements is

`20+bx-20-60=bx-60`

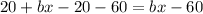
And we know that the final x position is -165. We deduce

`bx-60=-165 \iff bx = -165+60=-105`

(b) Similarly, we sum all the y displacements and we impose them to be equal to the final displacement:

`60-70+cy-70=59 \iff cy = 59-60+70+70 = 139`

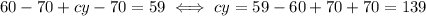
(c) The magnitude of the overall displacement is given by

`M = √((-165)^2+(59)^2)=√(27225+3481)=√(30706)\approx 175.23`

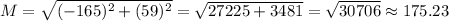
(d) The angle is given by

`\alpha = \arctan\left((59)/(-165)\right)+\pi \approx 2.8 \text{ radians}`