Question

The force F required to compress a spring a distance x is given by F 2 F0 5 kx where k is the spring constant and F0 is the preload. Determine the work required to compress a spring whose spring constant is k 5 200 lbf/in a distance of one inch starting from its free length where F0 5 0 lbf. Express your answer in both lbf·ft and Btu.

Answer 1

The work required to compress a spring with a spring constant of 200 lbf/in a distance of 1 inch from its free length is 8.33 lbf·ft or approximately 0.0107 Btu.

Step-by-step explanation:

To determine the work required to compress a spring, we can use the relationship W = 1/2kx², where W is the work done in foot-pounds (lbf·ft), k is the spring constant in pounds-force per inch (lbf/in), and x is the distance the spring is compressed in inches. For a spring constant of 200 lbf/in, compressing the spring a distance of 1 inch with an initial preload (F0) of 0 lbf, the work done is calculated as:

W = 1/2 × 200 lbf/in × (1 in)² = 100 lbf·in

To convert this to foot-pounds, we have:

100 lbf·in × (1 ft/12 in) = 8.33 lbf·ft

To express the work in British thermal units (Btu), we use the conversion factor that 1 Btu = 778 lbf·ft:

8.33 lbf·ft × (1 Btu/778 lbf·ft) ≈ 0.0107 Btu

Answer 2

a)W=8.333lbf.ft

b)W=0.0107 Btu.

Step-by-step explanation:

Complete question

The force F required to compress a spring a distance x is given by F– F0 = kx where k is the spring constant and F0 is the preload. Determine the work required to compress a spring whose spring constant is k= 200 lbf/in a distance of one inch starting from its free length where F0 = 0 lbf. Express your answer in both lbf-ft and Btu.

Solution

Preload = F₀=0 lbf

Spring constant k= 200 lbf/in

Initial length of spring x₁=0

Final length of spring x₂= 1 in

At any point, the force during deflection of a spring is given by;

F= F₀× kx where F₀ initial force, k is spring constant and x is the deflection from original point of the spring.

`W=\int\limits^2_1 {} \, Fds \\\\\\W=\int\limits^2_1( {F_0+kx} \,) dx \\\\\\W=\int\limits^a_b {kx} \, dx ; F_0=0\\\\\\W=k\int\limits^2_1 {x} \, dx \\\\\\W=k*(1)/(2) (x_2^(2)-x_1^(2)  )\\\\\\W=200*(1)/(2) (1^2-0)\\\\\\W=100.lbf.in\\\\`

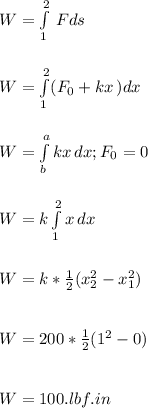
Change to lbf.ft by dividing the value by 12 because 1ft=12 in

100/12 = 8.333 lbf.ft

work required to compress the spring, W=8.333lbf.ft

The work required to compress the spring in Btu will be;

1 Btu= 778 lbf.ft

?= 8.333 lbf.ft----------------cross multiply

(8.333*1)/ 778 =0.0107 Btu.