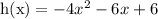Answer:
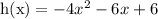
Explanation:
Given functions :
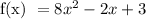 (1)
(1)
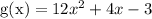 (2)
(2)
To find :
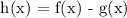
Consider :
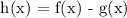
i.e. Subtract the expression for g(x) in equation (2) from the expression for f(x) in (1), we get
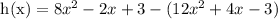
Multiply (-) sign inside the parentheses, we get
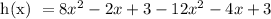
Combine like terms, we get
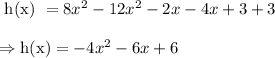
Hence, the correct answer is