Question

What is the minimum value of the objective function, C, with the given constraints?

C=2x+3y




A) 2x+3y≤24

B) 3x+y≤15

C) x≥2

D) y≥3

Answer 1

Given:

The objective function,
`C=2x+3y`,

Constraints,

`2x+3y\leq 24`

`3x+y\leq 15`

`x\geq 2`

`y\geq 3`

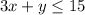
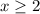
To find:

The minimum value of the given objective function.

Solution:

We have,

Objective function,
`C=2x+3y` ....(i)

The related equations of given constraints are

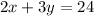`2x+3y=24` ...(ii)

`3x+y=15` ...(iii)

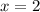`x=2`, it is a vertical line parallel to y-axis and 2 units left from y-axis.

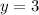`y=3`, it is a horizontal line parallel to x-axis and 4 units above from y-axis.

Table of value for (i),

x : 0 12

y : 8 0

Table of value for (ii),

x : 0 5

y : 15 0

Plot these points on a coordinate plane and draw these 4 related lines.

The sign of inequality of
`2x+3y\leq 24` and
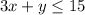`3x+y\leq 15` is ≤, it means the related lines are solid lines and the shaded region lie below the related line.

For
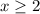`x\geq 2`, left side of the line
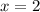`x=2` is shaded.

For
`y\geq 3`, shaded region is above the line
`y=3`.

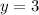From the below graph it is clear that the vertices of the feasible (common shaded region) are (2,3), (4,3), (3,6) and (2,6.667).

Points
`C=2x+3y`

(2,3)
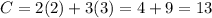`C=2(2)+3(3)=4+9=13` (Minimum)

(4,3)
`C=2(4)+3(3)=8+9=17`

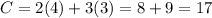
(3,6)
`C=2(3)+3(6)=6+18=24`

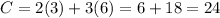
(2,6.667)
`C=2(2)+3(6.667)=4+20=24`

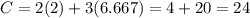
Therefore, the objective function is minimum at point (2,3).