Question

An important part of the customer service responsibilities of a cable company is the speed with which trouble in service can be repaired. Historically, the data show that the likelihood is 0.75 that troubles in a residential service can be repaired on the same day. For the first five troubles reported on a given day, what is the probability that fewer than two troubles will be repaired on the same day?

Answer 1

Answer: 0.015625

Explanation:

Binomial probability formula :_

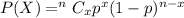`P(X)= ^nC_xp^x(1-p)^(n-x)`, where P(X) is the probability of getting success in x trials , p is the probability of getting success inn each trial and n is the sample size.

Given : The probability that troubles in a residential service can be repaired on the same day : p=0.75

Sample size : n=5

Then, the probability that fewer than two troubles will be repaired on the same day is given by:-

`P(X<2)=P(0)+P(1)\\\\=^5C_0(0.75)^0(0.25)^(5)+^5C_1(0.75)^1(0.25)^4\\\\=(1)(0.25)^5+(5)(0.75)(0.25)^4\ \ [\because\ ^nC_0=1\ \&\ ^nC_1=n]\\\\=0.0009765625+0.0146484375=0.015625`

Hence, the probability that fewer than two troubles will be repaired on the same day= 0.015625