Question

Cheetahs can accelerate to a speed of 19.6 m/s in 2.45 s and can continue to accelerate to reach a top speed of 27.6 m/s . Assume the acceleration is constant until the top speed is reached and is zero thereafter. Let the +x direction point in the direction the cheetah runs. Express the cheetah's top speed ????top in miles per hour (mi/h) .

Answer 1

• 
  `v_(top) = 61.96 (mi)/(h)`

Step-by-step explanation:

To express the cheetah's top speed in miles per hour, we just need to find the conversion factor.

We know that the top speed is

`v_(top) = 27.7 (m)/(s)`

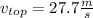
So, we want to obtain miles from meters and hours from seconds.

miles from meters

First we write the equivalence:

`1609.34 \ m = 1 \ mi`

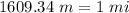
Now, we can divide by 1609.34 meters on both sides:

`(1609.34 \ m)/( 1609.34 \ m) = (1 \ mi)/( 1609.34 \ m)`

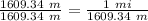
The left sides equals 1, so

`1 = (1 \ mi)/( 1609.34 \ m)`

And this is our conversion factor from meters to miles. Now, we can multiply our top speed by this conversion factor, as the conversion factor equals one, and is dimensionless, the physical meaning will be the same.

`v_(top) = 27.7 (m)/(s) * (1 \ mi)/( 1609.34 \ m)`

`v_(top) = 27.7 (m)/(s) * (1 \ mi)/( 1609.34 \ m)`

`v_(top) = 0.0172120 (mi)/(s)`

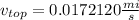
This is the top speed in miles per second, now, for obtaining miles per hour:

hours from seconds

We can do pretty much the same, first, the equivalence:

`1 \ h = 3600 \ s`

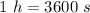
as the seconds are dividing in the velocity, we know divide by 1 hour.

`(1 \ h)/( 1 \ h) = (3600 \ s)/( 1 \ h)`

`1 = (3600 \ s)/( 1 \ h)`

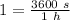
and know we just multiply our top speed by this conversion factor

`v_(top) = 0.0172120 (mi)/(s)  (3600 \ s)/( 1 \ h)`

`v_(top) = 61.96 (mi)/(h)`