DISCLAIMER: Please let me rename b and w the number of black and white balls, for the sake of readability. You can switch the variable names at any time and the ideas won't change a bit!
(a)
Case 1: both balls are white.
At the beginning we have
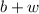 balls. We want to pick a white one, so we have a probability of
balls. We want to pick a white one, so we have a probability of
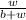 of picking a white one.
of picking a white one.
If this happens, we're left with
 white balls and still
white balls and still
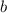 black balls, for a total of
black balls, for a total of
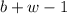 balls. So, now, the probability of picking a white ball is
balls. So, now, the probability of picking a white ball is
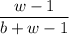
The probability of the two events happening one after the other is the product of the probabilities, so you pick two whites with probability
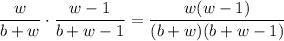
Case 2: both balls are black
The exact same logic leads to a probability of
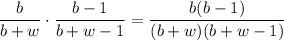
These two events are mutually exclusive (we either pick two whites or two blacks!), so the total probability of picking two balls of the same colour is
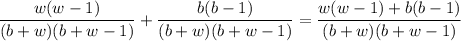
(b)
Case 1: both balls are white.
In this case, nothing changes between the two picks. So, you have a probability of
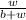 of picking a white ball with the first pick, and the same probability of picking a white ball with the second pick. Similarly, you have a probability
of picking a white ball with the first pick, and the same probability of picking a white ball with the second pick. Similarly, you have a probability
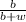 of picking a black ball with both picks.
of picking a black ball with both picks.
This leads to an overall probability of
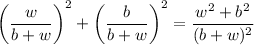
Of picking two balls of the same colour.
(c)
We want to prove that
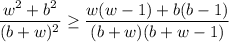
Expading all squares and products, this translates to
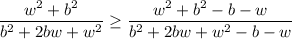
As you can see, this inequality comes in the form
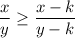
With x and y greater than k. This inequality is true whenever the numerator is smaller than the denominator:
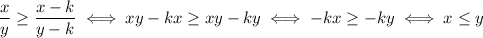
And this is our case, because in our case we have
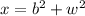
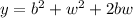 so, y has an extra piece and it is larger
so, y has an extra piece and it is larger
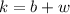 which ensures that k<x (and thus k<y), because b and w are integers, and so b<b^2 and w<w^2
which ensures that k<x (and thus k<y), because b and w are integers, and so b<b^2 and w<w^2