Question

What mass of Na2SO4 must be dissolved in 104 grams of water to lower the freezing point by 2.50 °C? The freezing point depression constant, Kfp, of water is –1.86 °C/m. Assume the van't Hoff factor for Na2SO4 is 2.88.

Answer 1

Answer: The mass of
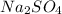`Na_2SO_4` that must be dissolved is 6.89 grams.

Step-by-step explanation:

Depression in freezing point is given by:

`\Delta T_f=i* K_f* m`

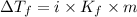
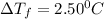`\Delta T_f=2.50^0C` = Depression in freezing point

i= vant hoff factor = 2.88

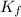`K_f` = freezing point constant =
`1.86^0C/m`

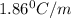
m= molality

`\Delta T_f=i* K_f* \frac{\text{mass of solute}}{\text{molar mass of solute}* \text{weight of solvent in kg}}`

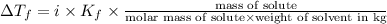
Weight of solvent (water)= 104 g = 0.104 kg

Molar mass of
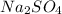`Na_2SO_4` = 142 g/mol

Mass of
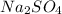`Na_2SO_4` added = ?

`2.50=2.88* 1.86* (x)/(142* 0.104)`

`x=6.89g`

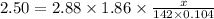
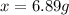
The mass of
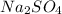`Na_2SO_4` that must be dissolved is 6.89 grams.