Question

Assume that trees are subjected to different levels of carbon dioxide atmosphere with 8% of the trees in a minimal growth condition at 350 parts per million (ppm), 11% at 440 ppm (slow growth), 48% at 560 ppm (moderate growth), and 33% at 640 ppm (rapid growth). What is the mean and standard deviation of the carbon dioxide atmosphere (in ppm) for these trees? The mean is ppm. [Round your answer to one decimal place (e.g. 98.7).] The standard deviation is ppm. [Round your answer to two decimal places (e.g. 98.76).]

Answer 1

Answer: The mean is 556.4 ppm.

The standard deviation is 84.92 ppm.

Explanation:

Let X denotes the concentration of carbon (ppm) .

Given :

X p(x)

350 0.08

440 0.11

560 0.48

640 0.33

The mean(expected value) is given by :-

`E[x]=\sum x p(x)`

`\Rightarrow\ E[x]=(350)(0.08)+(440)(0.11)+(560)(0.48)+(640)(0.33)=556.4`

Hence, the mean is 556.4 ppm.

Now,
`E[x^2]=\sum x^2 p(x)`

`\Rightarrow\ E[x]=(350)^2(0.08)+(440)^2(0.11)+(560)^2(0.48)+(640)^2(0.33)=316792`

`\text{Var(x)}=E[x^2]-[E[x]]^2\\\\=316792-556.4^2\\\\=316792-309580.96=7211.04`

Standard deviation:
`\sigma=√(7211.04)=84.9178426481\approx84.92`

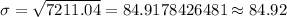
Hence, The standard deviation is 84.92 ppm.