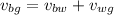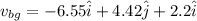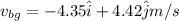Question

A 216-m-wide river flows due east at a uniform speed of 2.2 m/s. A boat with speed of 7.9 m/s relative to the water leaves the south bank of the river pointed in a direction 34 degrees west of north. What is the magnitude of the boat's velocity relative to the ground (in m/s)

Answer 1

The magnitude of the velocity of boat w.r.t ground is 6.2015 m/s

Solution:

As per the question;

Width of the river, w = 216 m

Uniform speed of boat due east,
`u_(x) = 2.2\hat{i} m/s`

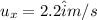
Angle in north west direction,
`\theta = 34^(\circ)`

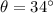
Velocity of the boat relative to water,
`v_(bw) = 7.9m/s`

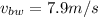
Now,

Velocity of the boat relative to the water is given by:

`v_(bw) = -7.9cos34^(\circ)\hat{i} + 7.9sin34^(\circ)\hat{j}`

`v_(bw) = - 6.55\hat{i} + 4.42\hat{j} m/s`

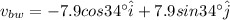
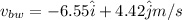
Also, velocity of water w.r.t ground is
`v_(wg) = u_(x) = 2.2\hat{i} m/s`

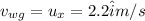
Now,

Magnitude of the velocity of boat w.r.t ground is given by:

`v_(bg) = v_(bw) + v_(wg)`

`v_(bg) = - 6.55\hat{i} + 4.42\hat{j} + 2.2\hat{i}`

`v_(bg) = - 4.35\hat{i} + 4.42\hat{j} m/s`

`|v_(bg)| = \sqrt{(- 4.35)^(2) + (4.42)^(2)} = 6.2015\ m/s`