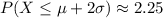Answer:
2.25 %
Step-by-step explanation:
65-95-99.7 is a rule to remember the precentages that lies around the mean.
at the range of mean (
 ) plus or minus one standard deviation (
) plus or minus one standard deviation (
 ),
),
![P([\mu-\sigma \leq X \leq \mu+\sigma])\approx 68.3%](https://img.qammunity.org/2020/formulas/physics/high-school/v03ycka6y8n48pocfldi331ffn28e6bfgy.png)
at the range of mean plus or minus two standard deviation,
![P([\mu -2\sigma \leq X \leq \mu+2\sigma])\approx 95.5%](https://img.qammunity.org/2020/formulas/physics/high-school/lg54bue75m2ho0qfe9drs579suy4mejxh7.png)
at the range of mean plus or minus three standard deviation,
![P([\mu - 3\sigma\leq X \leq \mu+3\sigma])\approx 99.7%](https://img.qammunity.org/2020/formulas/physics/high-school/b4bnytr0hognfozirsemlzm53m62wlm0gd.png)
So, note that they are asking about the probability that it is greater than 0.32, that is the mean (0.3) plus two times the standard deviation (0.1) (
 )
)
So we know that the 95.5% is between
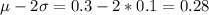 and
and
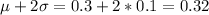 , hence approximately the 4.5% (100%-95.5%) is greater than 0.32 or less than 0.28. But half (4.5%/2=2.25%) is greater than 0.32 and the other half is less than 0.28.
, hence approximately the 4.5% (100%-95.5%) is greater than 0.32 or less than 0.28. But half (4.5%/2=2.25%) is greater than 0.32 and the other half is less than 0.28.
So