Question

A baker bakes a batch of muffins and splits the batch evenly onto six different trays. She then adds five croissants to each tray. If each tray now contains at least twenty baked goods, what is the least possible number of muffins in the baker's original batch?

Answer 1

90

Explanation:

Answer 2

90

Explanation:

Using inequalities we can understand this problem.

First call X the number of products in the original batch

Then X/6 is the number of muffins in each tray before putting the croissants

Finally, X/6+5 are the products in each tray counting the croissants, and this quantity at least should be 20, it means:

`(X)/(6)+5\geq 20`

Isolating X:

`(X)/(6)\geq 20-5\\(X)/(6)\geq 15\\X\geq 6*15\\X\geq 90`

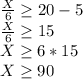
The least possible number of muffins in the baker's original batch is 90.