Question

Ask Your Teacher Cam Newton of the Carolina Panthers throws a perfect football spiral at 6.9 rev/s. The radius of a pro football is 8.5 cm at the middle of the short side. What is the centripetal acceleration of the laces on the football? (Enter the magnitude in m/s2.)

Answer 1

`a=159.32\ m/s^2`

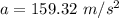
Step-by-step explanation:

It is given that,

Angular speed of the football spiral,
`\omega=6.9\ rev/s=43.35\ rad/s`

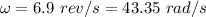
Radius of a pro football, r = 8.5 cm = 0.085 m

The velocity is given by :

`v=r\omega`

`v=0.085* 43.35`

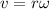
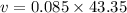
v = 3.68 m/s

The centripetal acceleration is given by :

`a=(v^2)/(r)`

`a=((3.68)^2)/(0.085)`

`a=159.32\ m/s^2`

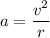
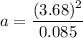
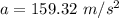
So, the centripetal acceleration of the laces on the football is
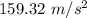`159.32\ m/s^2`. Hence, this is the required solution.