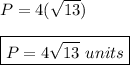Question

On a coordinate plane, rhombus W X Y Z is shown. Point W is at (7, 2), point X is at (5, negative 1), point Y is at (3, 2), and point Z is at (5, 5). What is the perimeter of rhombus WXYZ? StartRoot 13 EndRoot units 12 units StartRoot 13 EndRoot units D)>20 units

Answer 1

4 13

Explanation:

Answer 2

Shown in the explanation

Explanation:

A Rhombus is a quadrilateral having four sides of equal length each. Here, we know that the vertices of this shape are:

`W(7,2) \\ \\ X(5,-1) \\ \\ Y(3,2) \\ \\ Z(5,5)`

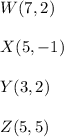
So the rhombus is named as WXYZ. To find its perimeter (P), we just need to find the length of one side and multiply that value by 4. By using the distance formula, we know that:

`\overline{WX}=\sqrt{(x_(1)-x_(2))^2+(y_(1)-y_(2))^2} \\ \\ W(7,2)=W(x_(1),y_(1)) \\ \\ X(5,-1)=X(x_(2),y_(2)) \\ \\ \\ \overline{WX}=√((7-5)^2+(2-(-1))^2) \\ \\  \overline{WX}=√((2)^2+(3)^2) \\ \\ \overline{WX}=√(4+9) \\ \\ \overline{WX}=√(13)`

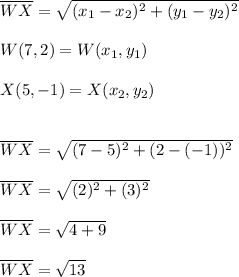
Finally, the Perimeter (P) is:

`P=4(√(13)) \\ \\ \boxed{P=4√(13)\ units}`