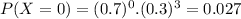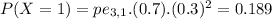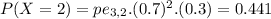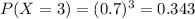Question

In a semiconductor manufacturing process, three wafers from a lot are tested. Each wafer is classified as pass or fail. Assume that the probability that a wafer passes the test is 0.7 and that wafers are independent. Determine the probability mass function of the number of wafers from a lot that pass the test. Round your answers to three decimal places (e.g. 98.765).

Answer 1

`P(X = 0) = 0.027`

`P(X = 1) = 0.189`

`P(X = 2) = 0.441`

`P(X = 3)= 0.343`

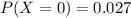
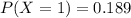
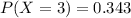
Explanation:

The probability mass function P(X = x) is the probability that X happens x times.

When n trials happen, for each
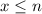`x \leq n`, the probability mass function is given by:

`P(X = x) = pe_(n,x).p^(x).(1-p)^(n-x)`

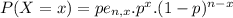
In which p is the probability that the event happens.

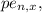`pe_(n,x),` is the permutation of n elements with x repetitions(when there are multiple events happening(like one passes and two not passing)). It can be calculated by the following formula:

`pe_(n,x) = (n!)/(x!)`

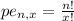
The sum of all P(X=x) must be 1.

In this problem

We have 3 trials, so
`n = 3`

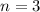
The probability that a wafer pass a test is 0.7, so
`p = 0.7`

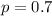
Determine the probability mass function of the number of wafers from a lot that pass the test.

`P(X = 0) = (0.7)^(0).(0.3)^(3) = 0.027`

`P(X = 1) = pe_(3,1).(0.7).(0.3)^(2) = 0.189`

`P(X = 2) = pe_(3,2).(0.7)^(2).(0.3) = 0.441`

`P(X = 3) = (0.7)^(3) = 0.343`