Question

You are climbing in the High Sierra when you suddenly find yourself at the edge of a fog-shrouded cliff. To find the height of this cliff, you drop a rock from the top; 7.40 s later you hear the sound of the rock hitting the ground at the foot of the cliff. Part APart complete If you ignore air resistance, how high is the cliff if the speed of sound is 330 m/s? Express your answer with the appropriate units.

Answer 1

221.5 m

Step-by-step explanation:

Let h be the height of the cliff

t = Time taken by the stone to fall to the ground

Time taken to hear the sound is 7.4 seconds

Time taken by the sound to travel the height of the cliff = 7.4-t

Speed of sound in air = 330 m/s

For the stone falling

`s=ut+(1)/(2)at^2\\\Rightarrow h=0t+(1)/(2)* 9.81* t^2\\\Rightarrow h=(1)/(2)* 9.81* t^2`

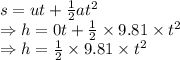
For the sound

Distance = Speed × Time

`\text{Distance}=330* (7.4-t)`

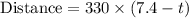
Here, distance travelled by the stone and sound is equal

`(1)/(2)* 9.81* t^2=330* (7.4-t)\\\Rightarrow 4.905t^2=330* (7.4-t)\\\Rightarrow t^2=(330)/(4.905)(7.4-t)\\\Rightarrow t^2+67.28t-497.872=0\\\Rightarrow 1000t^2+67280t-497872=0`

`t=(-67280+√(67280^2+1991488000))/(2000),\:t=(-67280-√(67280^2+1991488000))/(2000)\\\Rightarrow t=6.72\ s\ or\ -74\ seconds`

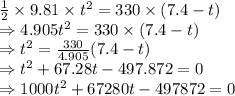
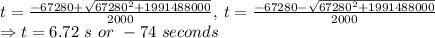
The time taken to fall down is 6.72 seconds

`h=(1)/(2)* 9.81* 6.72^2=221.5\ m`

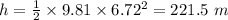
Height of the cliff is 221.5 m