Question

Using traditional methods, it takes 99 hours to receive a basic flying license. A new license training method using Computer Aided Instruction (CAI) has been proposed. A researcher used the technique with 80 students and observed that they had a mean of 100 hours. Assume the variance is known to be 25. A level of significance of 0.05 will be used to determine if the technique performs differently than the traditional method. Is there sufficient evidence to support the claim that the technique performs differently than the traditional method?

Answer 1

Answer with explanation:

Let
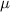`\mu` be the population mean.

By considering the given information , we have

Null hypothesis :
`H_0: \mu=99`

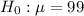
Alternative hypothesis :
`H_0: \mu\\eq99`

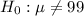
Since alternative hypothesis is two-tailed , so the test is a two-tailed test.

Given : Sample size : n=80 ;

Sample mean:
`\overline{x}=100` ;

Standard deviation:
`s=√(Var)=√(25)=5`

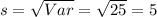
Test statistic for population mean:

`z=\frac{\overline{x}-\mu}{(s)/(√(n))}`

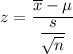
i.e.
`z=(99-100)/((5)/(√(80)))\approx-1.79`

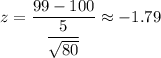
Using the standard normal distribution table of z , we have

P-value for two tailed test :
`2P(Z>|z|)=2(1-P(Z<|z|))`

`=2(1-P(z<1.79))=2(1-0.963273)=0.073454`

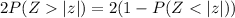
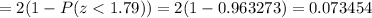
Since , the P-value is greater than the significance level of
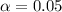`\alpha=0.05` , it means we do not have sufficient evidence to reject the null hypothesis.

Hence, we conclude that we do not have enough evidence to support the claim that the technique performs differently than the traditional method.