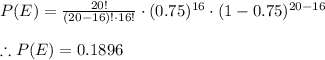Question

The probability that your call to a service line is answered in less than 30 seconds is 0.75. Assume that your calls are independent. (a) If you call 11 times, what is the probability that exactly 9 of your calls are answered within 30 seconds? Round your answer to four decimal places (e.g. 98.7654). (b) If you call 20 times, what is the probability that at least 16 calls are answered in less than 30 seconds? Round your answer to four decimal places (e.g. 98.7654). (c) If you call 26 times, what is the mean number of calls that are answered in less than 30 seconds? Round your answer to the nearest integer.

Answer 1

Answer with Step-by-step explanation:

Since the given event is binary we can use Bernoulli's probability to sove the problem

Thus for an event 'E' with probability of success 'p' the probability that the event occurs 'r' times in 'n' trails is given by

`P(E)=(n!)/((n-r)!\cdot r!)\cdot p^(r)\cdot (1-p)^(n-r)`

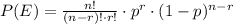
Part a)

For part a n = 11 , r =9, p = 0.75

Applying values we get

`P(E)=(11!)/((11-9)!\cdot 9!)\cdot (0.75)^(9)\cdot (1-0.75)^(11-9)\\\\\therefore P(E)=0.2581`

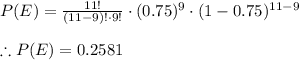
Part b)

For part b n = 20 , r = 16 , p=0.75

Applying values we get

`P(E)=(20!)/((20-16)!\cdot 16!)\cdot (0.75)^(16)\cdot (1-0.75)^(20-16)\\\\\therefore P(E)=0.1896`