Which of the following gives an equation of a line that passes through the point (,-19) and is parallel to the line that passes through the origin and point (-2, -12)?

Question

asked Dec 10, 2020 155k views

1 Answer

Sutee · Answer 1 · 2020-12-15T14:35:06+0000

Answer:

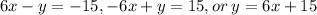
$\displaystyle 6x - y = -15, -6x + y = 15, or\:y = 6x + 15$

Explanation:

First, find the rate of change [slope]:

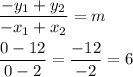
$\displaystyle (-y_1 + y_2)/(-x_1 + x_2) = m \\ \\ (0 - 12)/(0 - 2) = (-12)/(-2) = 6$

Then plug [−1, 9] into the Slope-Intercept Formula instead of the Point-Slope Formula because you get it done much more swiftly:

9 = 6[−1] + b

−6

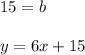
$\displaystyle 15 = b \\ \\ y = 6x + 15$

If you want it in Standard Form:

y = 6x + 15

- 6x - 6x

__________

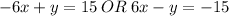
$\displaystyle -6x + y = 15\:OR\:6x - y = -15$

I am joyous to assist you anytime.