Question

Write an expression to describe the sequence below. Use n to represent the position of a term in the sequence, where n = 1 for the first term.

-95, -190, -285, -380, ...

Please show how you got the answer, I want to use it for further examples to solve problems like this myself. Thank you.

Answer 1

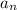`a_(n)` = - 95n

Explanation:

Note the difference between consecutive terms in the sequence is constant

- 190 - (- 95) = - 190 + 95 = - 95

- 285 - (- 190) = - 285 + 190 = - 95

- 380 - (- 285) = - 380 + 285 = - 95

This indicates that the terms are an arithmetic sequence with n th term

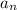`a_(n)` = a₁ + (n - 1)d

where a₁ is the first term and d the common difference

Here a₁ = - 95 and d = - 95, thus

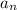`a_(n)` = - 95 - 95(n - 1) = - 95 - 95n + 95 = - 95n