A graph that shows the boat's value increasing at a rate of 25% per year is: D. graph D.
In Mathematics and Statistics, a population or material that increases at a specific period of time represents an exponential growth.
This ultimately implies that, a mathematical model for any population or material that increases by "b" percent per unit of time is an exponential function of this form:
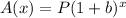
Where:
- A(x) represents the future value.
- P represents the initial value.
- b represents the rate of change or growth rate.
- x represents the time.
Since the boat's value is increasing at a rate of 25% per year, we can reasonably infer and logically deduce that its growth rate is as follows;
Growth rate, b = 1 + (25/100)
Growth rate, b = 1.25
By using the parent function, the required exponential growth rate function is given by;
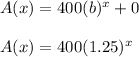
In conclusion, only graph D correctly show a boat's value that is increasing at a rate of 25% per year.