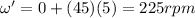Question

a fan acquires a speed of 180 rpm in 4s, starting from rest. calculate the speed of the fan at the end of the 5th second starting from rest. Assume angular acceleration to be uniform

Answer 1

225 rpm

Step-by-step explanation:

The angular acceleration of the fan is given by:

`\alpha = (\omega_f - \omega_i)/(\Delta t)`

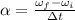
where

`\omega_f` is the final angular speed

`\omega_i` is the initial angular speed

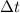`\Delta t` is the time interval

For the fan in this problem,

`\omega_i = 0\\\omega_f = 180 rpm\\\Delta t=4 s`

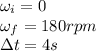
Substituting,

`\alpha = (180-0)/(4)=45 rpm/s`

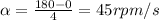
Now we can find the angular speed of the fan at the end of the 5th second, so after t = 5 s. It is given by:

`\omega' = \omega_i + \alpha t`

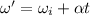
where

`\omega_i = 0\\\alpha = 45 rpm/s\\t = 5 s`

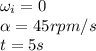
Substituting,

`\omega' = 0 + (45)(5)=225 rpm`