Answer:
True.
Explanation:
The given expression is
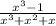
This expression is rational, which means the denominator must be different to zero, otherwise, the function will be undefined. So, let's find if there are values that make the denominator zero.
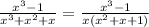
So, if we evaluate the expression with
 , we would have
, we would have
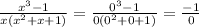
As you can observe, there must be one exclusion, because it makes the expression undefined.
Therefore, the answer is true.