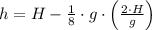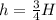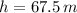Question

Please help asap!!

Assume that the cannon is fired at time t=0 and that the cannonball hits the ground at time tg. What is the y position of the cannonball at the time tg/2?
Answer numerically in units of meters.

Answer 1

Step-by-step explanation:

Let's use the equation Δy =
`v(t)-(1)/(2)(g)(t)^(2)`

That would mean -h =
`v((9.8)/(2))-(1)/(2)(9.80)((9.8)/(2))^(2).</p><p>Since the ball has stopped at t = 9.8 = g, then that would mean that the final velocity v = 0.</p><p>-h = [tex](0)((9.8)/(2))-((1)/(2))(9.80)((9.8)/(2))^(2)`

`h = -((1)/(2))(9.80)((9.8)/(2))^(2)`

`h = ((1)/(2))(9.80)((9.8)/(2))^(2)`

`h = ((9.8)/(2))((9.8)/(2))((9.8)/(2))`

`h = (9.8^(3))/(2^(3))`

`h = (941.192)/(8)`

`h = 117.649`

The height of the cannonball at
`t = (9.8)/(2)` should be 117.649 m

Hope this helps!

Answer 2

`h = 67.5\,m`

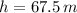
Step-by-step explanation:

The position of the cannonball is given by the following expressions:

Half position

`h = H -(1)/(2)\cdot g \cdot \left((t_(g))/(2) \right)^(2)`

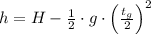
Final position

`0 = H -(1)/(2)\cdot g \cdot t_(g)^(2)`

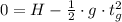
The instant when the cannonball hits the ground is:

`t_(g) = \sqrt{(2\cdot H)/(g) }`

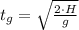
Lastly, this result is applied in the other equation, which simplified afterwards:

`h = H -(1)/(8)\cdot g \cdot \left((2\cdot H)/(g) \right)`

`h = H -(1)/(4)\cdot H`

`h = (3)/(4)H`

`h = 67.5\,m`