Question

The base of 40-foot ladder is 8 feet from the wall. How high is the ladder on the wall (round to the nearest foot)

Answer 1

Given:

The base of 40-foot ladder is 8 feet from the wall.

To find:

How high is the ladder on the wall (round to the nearest foot).

Solution:

Ladder makes a right angle triangle with wall and ground.

We have,

Length of ladder (hypotenuse)= 40 foot

Base = 8 foot

We need to find the perpendicular to get the height of the ladder on the wall.

Let h be the height of the ladder on the wall.

According to the Pythagoras theorem,

`Hypotenuse^2=Base^2+Perpendicular^2`

`(40)^2=(8)^2+(h)^2`

`1600=64+h^2`

`1600-64=h^2`

`1536=h^2`

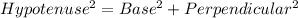
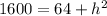
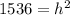
Taking square root on both sides.

`\pm √(1536)=h`

`\pm 39.1918358=h`

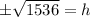
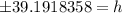
Height cannot be negative. Round to the nearest foot.

`h\approx 39`

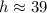
Therefore, the height of the ladder on the wall is 39 foot.