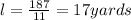Question

A rectangle is 6yards longer than it is wide. Find the dimensions of the rectangle if it’s area is 187 square yards

Answer 1

Width = 11 yards

Length = 17 yards

Explanation:

First of all, the length of the rectangle is 6 yards longer than the width, this means, length = width + 6 yards. This dimensions can be represented on figure 1, where w is width, and l, for length.

We know the area of a rectangle is A = width x length

For our case 187 = w . (w + 6)

Using the Distributive Property for the multiplication we obtain

`187 = w^(2) +6w`

`w^(2) +6w-187 =0,`

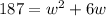
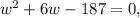
Using the quadratic formula
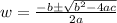`w=\frac{-b\±\sqrt{b^(2)-4ac } }{2a}` where a = 1, b = 6, c = - 187 and replacing into the formula, we will have:

`w=(-6\±√(6^2-4(1)(-187)) )/(2(1))`

`w=(-6\±√(36+748) )/(2)=(-6\±√(784) )/(2)=(-6\±28)/(2)`

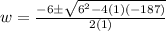
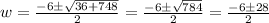
We have two options:
`w=(-6+28)/(2)=(22)/(2)=11  yards`

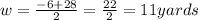
Or

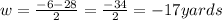`w=(-6-28)/(2)=(-34)/(2)=-17 yards` But a distance (width) can not be negative so, this answer for w must be discarded.

The answer must be width = 11 yards.

To find the length
`l =(187)/(11)=17 yards`