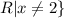Answer:
The domain is
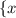 ∈
∈
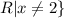
Explanation:
Given the fucntion
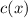 :
:
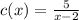
And the function
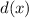 :
:
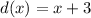
You must multiply them in order to get
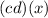 . Then, this is:
. Then, this is:
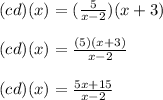
You can notice that it is a Rational function.
Since the denominator cannot be zero, the domain of this function will be all the real numbers except those that makes the denominator zero.
Then, you must equate the denominator to zero and solve for "x":
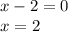
Therefore, the domain is
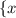 ∈
∈