Answer:
Thunderbird is 995.157 meters behind the Mercedes
Step-by-step explanation:
It is given that all the cars were moving at a speed of 71 m/s when the driver of Thunderbird decided to take a pit stop and slows down for 250 m. She spent 5 seconds in the pit stop.
Here final velocity
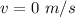
initial velocity
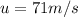 distance
distance
Distance covered in the slowing down phase =
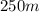
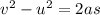
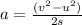
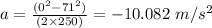

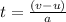
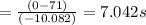
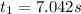
The car is in the pit stop for 5s
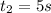
After restart it accelerates for 350 m to reach the earlier velocity 71 m/s
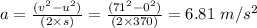

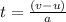
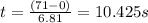

total time=
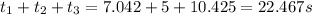
Distance covered by the Mercedes Benz during this time is given by

Distance covered by the Thunderbird during this time=
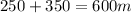
Difference between distance covered by the Mercedes and Thunderbird
=
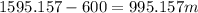
Thus the Mercedes is 995.157 m ahead of the Thunderbird.