Final Answer:
The function g(x) is g(x) =
 .
.
Step-by-step explanation:
To find the function g(x), we'll use the given information that (f+g)(x) = 6 -
 and f(x) = 3x + 1. The expression (f+g)(x) represents the sum of the functions f(x) and g(x).
and f(x) = 3x + 1. The expression (f+g)(x) represents the sum of the functions f(x) and g(x).
Start by substituting the expression for f(x) into the sum:
(f+g)(x) = f(x) + g(x) =
 .
.
Replace f(x) with (3x + 1): 3x + 1 + g(x) = 6 -
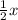 .
.
Now, isolate g(x) by moving the terms involving g(x) to one side: g(x) = 6 -
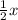 - 3x - 1.
- 3x - 1.
Combine like terms and simplify: g(x) =
 - 3x + 6 - 1.
- 3x + 6 - 1.
Further simplify to obtain the final answer: g(x) =
 - 5.
- 5.
In summary, the function g(x) is found by subtracting the expression for f(x) from the sum given in the problem. The steps involve substituting the known expression for f(x), isolating the terms involving g(x), and simplifying the result to obtain the final function for g(x), which is g(x) = -
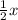 - 5.
- 5.