Question

If you push a crate horizontally with 100 N across a 10 m factory floor and the friction between the crate and the floor is a steady 70 N, how much kinetic energy does the crate gain?

Answer 1

300 j

Step-by-step explanation:

Answer 2

300 J

Step-by-step explanation:

First of all, we need to calculate the net force acting on the crate, which is given by:

`F_(net) = F-F_f`

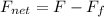
where

F = 100 N is the horizontal push

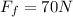`F_f = 70 N` is the force of friction

Substituting,

`F_(net)=100 - 70 = 30 N`

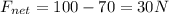
Now we can calculate the net work done on the crate:

`W=F_(net)d`

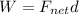
where

d = 10 m is the displacement

Substituting,

`W=(30)(10)=300 J`

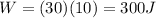
According to the work-energy theorem, the kinetic energy gained by the crate is equal to the work done on it: therefore, the answer is 300 J.