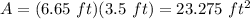Answer:
-
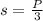
- Dimensions of the flag:
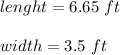
- Area of the flag:
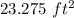
Explanation:
The missing figure of the exercise is attached.
We know that the perimeter of the triangle is given by:
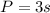
Where "s" is the side lenght of the triangle.
Solving for "s", we get:
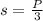
Therefore, if the perimeter of the triangle is 126 inches, its side length is:
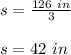
Since
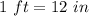 , we know that "s" in feet is:
, we know that "s" in feet is:
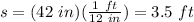
The area of a rectangle can be calculated with this formula:
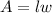
Where "l" is the lenght and "w" is the width
We can observe in the figure that the lenght and the width of the flag are:
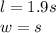
Then, the dimensions of the flag are:
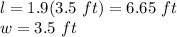
And the area is: