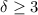Answer:

Explanation:
As 2 and 7 are the only prime divisors of both
 and
and
 we know that both can be written as:
we know that both can be written as:
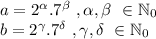
Where
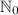 is the set of all natural numbers adding the zero (careful because this part is important as I'll explain next).
is the set of all natural numbers adding the zero (careful because this part is important as I'll explain next).
We also know that 14 divides both numbers and that is actually the greatest common divisor between them. So we can rewrite a and b as follows:
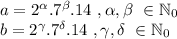
Why do I write them like this? Because this way is easier to observe that if
 and
and
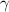 were both greater than zero, then 28 would divide both hence 14 wouldn't be their g.c.d.. Likewise, if
were both greater than zero, then 28 would divide both hence 14 wouldn't be their g.c.d.. Likewise, if
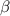 and
and
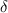 were both greater than zero, then 98 would divide both and once again, 14 wouldn't be their g.c.d.
were both greater than zero, then 98 would divide both and once again, 14 wouldn't be their g.c.d.
So either of them has to be equal to zero. And then we have that
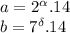
All we have left to do is find the possible values for
 and
and
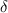 so that
so that
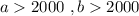 and that only happens if
and that only happens if
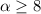 and
and