Question

Diffraction of sound waves is demonstrated when sound waves with a frequency of 1300 Hz from a distant source are diffracted through a doorway which is 84 cm wide. Calculate the angle between the first two orders of diffraction taking the speed of sound to be 343 m/s.

Answer 1

39.05°

Step-by-step explanation:

As we know that, the diffraction is the phenomena of bending of light when it passes through an obstacle.

Mathematically,

`dsin\theta=n\lambda`

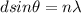
Here, d is slit width,
`\lambda` is the wavelength, n is the order,
`\theta` is the angle.

Given that, d is 84 cm, n is 2, and the wavelength can be calculated as,

`\lambda=(c)/(f)`

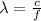
Here, c is the speed of sound and f is the frequency of sound wave.

Here, c is 343 m/s and f is 1300 Hz,

Therefore,

`\lambda=(343 m/s)/(1300 Hz)\\\lambda=0.264m`

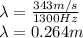
Recall diffraction equation in term of
`sin\theta`.

`sin\theta=(n\lambda)/(d)`

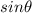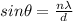
Put all the variables.

`sin\theta=(2* 0.264 m)/(84 cm)\\sin\theta=(2* 0.264 m)/(0.84 m)\\\theta=39.05^(\circ)`

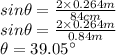
Therefore, it is the required angle between the first 2 order of diffraction.