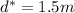Question

A swimming pool is filled to a depth of 2.0 m. How deep does the pool appear to be from above the water, which has an index of refraction of 1.33? (A) 1.5 m (B) 1.33 m (C) 2.5 m (D) 1.5 cm

Answer 1

Answer: (A) 1.5 m

Step-by-step explanation:

This situation is due to Refraction, a phenomenon in which a wave (the light in this case) bends or changes its direction when passing through a medium with an index of refraction different from the other medium.

In this context, the index of refraction is a number that describes how fast light propagates through a medium or material.

In addition, we have the following equation that states a relationship between the apparent depth
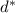`{d}^(*)` and the actual depth
`d`:

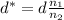`{d}^(*)=d\frac{{n}_(1)}{{n}_(2)}` (1)

Where:

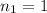`n_(1)=1` is the air's index of refraction

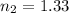`n_(2)=1.33` water's index of refraction.

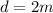`d=2 m` is the actual depth of water

Now. when
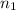`n_(1)` is smaller than
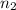`n_(2)` the apparent depth is smaller than the actual depth. And, when
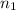`n_(1)` is greater than
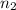`n_(2)` the apparent depth is greater than the actual depth.

Let's prove it:

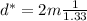`{d}^(*)=2 m(1)/(1.33)` (2)

Finally we find the apparent depth of water, which is smaller than the actual depth:

`{d}^(*)=1.5 m`