Question

Segment AB is the hypotenuse of the right isosceles ΔABC with A(2, 3) and B(7, 3). Find all possible coordinates of C.

Can you also please add how you solved it? Im clueless :/

Answer 1

Answer: c(4.5,5.5) or c(4.5,0.5)

Explanation:

Mac=y-3/4.5-2=y-3/2.5

Mbc=y-3/4.5-7=y-3/-2.5

Answer 2

The possible coordinates of point C are (4.5 , 5.5) OR (4.5 , 0.5)

Explanation:

* Lets explain how to solve the problem

- The problems it seems that difficult but if you think about the

properties of the isosceles triangle

∵ AB is the hypotenuse of the right isosceles Δ ABC

∴ The equal sides are AC and BC

∵ A = (2 , 3) and B = (7 , 3)

- The y-coordinates of A and B are equal then, AB is a horizontal

segment

∴ The vertical segment drawn from point C to the hypotenuse AB

will bisect it

∴ The x-coordinate of point c equal the x-coordinate of the mid-point

of AB

∵ The x-coordinate of the mid-point of AB is half the sum of

x-coordinates of points A and B

∴ The x-coordinate of point C is
`x=(2+7)/(2)=(9)/(2)=4.5`

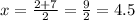
∴ The x-coordinate of point C is 4.5

∴ C = (4.5 , y)

* Now lets think about the slopes of the perpendicular lines

- The product of the slopes of the perpendicular line is -1

∵ ΔABC is isosceles right triangle, where m∠C = 90°

∴ AC ⊥ BC

- Lets find the slopes of AC and BC

∵ A = (2 , 3) , B = (7 , 3) and C = (4.5 , y)

∵
`m_(AC)=(y-3)/(4.5-2)=(y-3)/(2.5)`

∵
`m_(BC)=(y-3)/(4.5-7)=(y-3)/(-2.5)`

∵
`m_(AC)*m_(BC)=-1`

∴
`(y-3)/(2.5)*(y-3)/(-2.5)=-1`

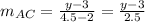
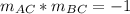
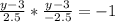
- By using cross multiplication

∴ (y - 3)² = - 2.5 × 2.5 × -1

∴ (y - 3)² = 6.25

- By taking √ for both sides

∴ y - 3 = ± 2.5

∴ y - 3 = 2.5 OR y - 3 = -2.5

∵ y - 3 = 2.5 ⇒ add 3 to both sides

∴ y = 5.5

OR

∵ y - 3 = -2.5 ⇒ add 3 to both sides

∴ y = 0.5

∴ The y-coordinates of point C are 5.5 or 0.5

* The possible coordinates of point C are (4.5 , 5.5) OR (4.5 , 0.5)