Answer:
The final speed of cart with mass 0.06 kg is 2.7 m/s and the final speed of the cart of mass 0.09 kg is 4.2 m/s.
Step-by-step explanation:
Initial moumentum of cart with mass 0.06 kg is
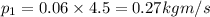
Initial moumentum of cart with mass 0.06 kg is

Thus initial moumentum of system is
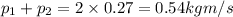
Now let the final velocity of 0.06 kg cart be
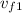 and that of 0.09 kg cart be
and that of 0.09 kg cart be
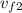
Thus final moumentum of system is
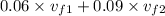
Equating initial and final values we get
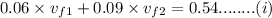
Similarly conserving the kinetic energies of the 2 carts we get
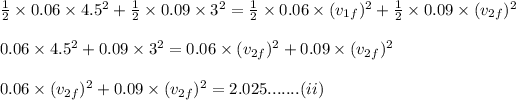
Solving equation i and ii we get
Substituting value of
 from i and using it in equation ii we get
from i and using it in equation ii we get
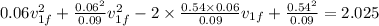
Solving for
 we get
we get
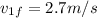
Similarly
