Question

3. As part of your weight training regimen, you want to consume lean sources of protein. You want consume at least 300 Calories a day from at least 48 grams of protein. One ounce of chicken provides 35 Calories and 8.5 g of protein. One ounce of tofu provides 20 Calories and 2.5 g of protein. Your local supermarket charges $5 a pound for chicken and $2.5 a pound for tofu. How much of each food should you eat each day if you want to meet your requirements with the lowest cost? What is this daily cost?

Answer 1

Let x ounce of chicken and y ounce of tofu were taken,

∵ One ounce of chicken provides 35 Calories and 8.5 g of protein,

So, in x ounces of chicken

Calories = 35x, Protein = 8.5x grams,

Now, One ounce of tofu provides 20 Calories and 2.5 g of protein.

So, in y ounces of tofu,

Calories = 20y and protein = 2.5y grams,

Thus, the total calories = 35x + 20y,

Total protein = 8.5x + 2.5y

According to the question,

35x + 20y ≥ 300 -----(1),

8.5x + 2.5y ≥ 48 ----(2),

Now, the cost of a pound for chicken = $ 5,

So, the cost of 16 ounces of chicken = $ 5 ( ∵ 1 pound = 16 ounces ),

⇒ the cost of 1 ounces of chicken =
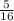`(5)/(16)` dollars,

Similarly, the cost of a pound of tofu = $ 2.5,

So, the cost of 1 ounces of tofu =
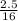`(2.5)/(16)` dollars,

Thus, the total cost of x ounces of chicken and y ounces of tofu

`C=(5)/(16)x+(2.5)/(16)y`

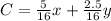
Now, by graphing the above constraints ( by equation (1) and (2) )

We get a feasible region that shows the possible values of x and y,

The boundary points of the feasible region are,

(2.545, 10.545), (0, 19.2), (8.571, 0)

`C=(5)/(16)* 2.545+(2.5)/(16)* 10.545 = 2.443`

`C=(5)/(16)* 0+(2.5)/(16)* 19.2 = 3`

`C=(5)/(16)* 8.571+(2.5)/(16)* 0 = 2.678`

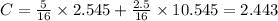
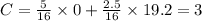
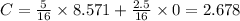
Hence, the minimum cost is $ 2.443,

For which 2.545 ounces of chicken and 10.545 ounces of tofu should be eaten.