Question

Find the area of the triangle formed by the origin and the points of intersection of the parabolas with equations y=−3x2+20 and y=x2−16 .

Answer 1

Area = 21 unit²

Explanation:

We have one point of triangle = (0,0)

The other points can be solved, intersection means

−3x²+20 = x²−16

4x² = 36

x² = 9

x = ±3

when x = 3, y = 3²−16 = 9 -16 = -7 , point is (3,-7)

when x = -3, y = (-3)²−16 = 9 -16 = -7 , point is (-3,-7)

We need to find area of triangle with points (0,0), (3,-7) and (-3,-7).

Area of triangle is given by

`Area =(1)/(2)\begin{vmatrix}0 & 0 & 1\\ 3 & -7 & 1\\ -3 & -7 & 1\end{vmatrix}`

`Area = (1)/(2)\left ( 0(-7* 1-(1* -7))-0(3* 1-(1* -3))+1(3* -7-(-3* -7)\right )\\\\Area =(1)/(2)(-21-21)=-21=21unit^2`

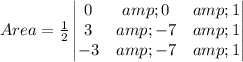
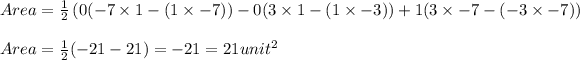
Area = 21 unit²