Question

Sketch T-s and p-v diagrams for the Otto cycle.

Answer 1

see picture

Step-by-step explanation:

The Otto cycle is a theoretical approach to the explosion motors (the ones in most cars). It’s a process that includes 4 steps.

1. Admission (A-B): here the piston goes down to allow the mix (air +fuel) enter in combustion camera. In this process the pressure, since the piston is open, is constant but volume is increasing. Temperature and entropy are constant (not temperature change, not entropy change here)

2. Compression (1-2): Here the piston goes up to compress the mix (air +fuel). Since this process is very fast we can say that there is no heat exchange so, it’s an adiabatic process. Both pressure and volume are changing. Temperature raises but entropy is constant because it is an adiabatic process.

3. Combustion (2-3): when the mix has reached a certain temperature (ignition temperature) the combustion of the mix (air+ fuel) occurs. We can consider that the volume is constant because the process is very fast while both temperature and pressure are increasing. The entropy can be estimated using the expression for entropy while volume is constant

`S=n*c_(v)*ln((T)/(T_(0))) + n*R*ln((V)/(V_(0)))`

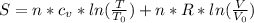
Clearing T from the expression we have:

`T=T_(0)((V)/(V_(0)))^(y-1) e^{(S)/(nc_(v))}`

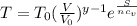
When V is constant the temperature and entropy are related in an exponential behavior.

4. Expansion (3-4): The high temperature makes the piston goes down increasing the volume and decreasing the pressure of the system. Since this process occurs very fast we can say that there is no heat exchange so it’s adiabatic and the entropy is constant.

5. Escape (4-1): In this step, the combustion gases leaves the combustion camera (at high temperature) and are replaced with another admission of the mix (air+fuel) (low temperature). Since the among of mix that leaves the system is the same that enter in it, we can say that the volume remains constant while temperature and pressure decrease. The entropy keeps the exponential relationship with temperature for a process where volume is constant.