Question

The graph of a function is shown. On a coordinate plane, a function has 2 connecting line. The first line goes from (negative 5, negative 2) to (0, 3). The second line starts at (0, 3) and continues horizontally at y = 3. Which function is represented by the graph? f(x) = StartLayout enlarged left-brace 1st Row 1st column x minus 3, 2nd column x less-than 0 2nd Row 1st column 3, 2nd column x greater-than-or-equal-to 0 EndLayout f(x) = StartLayout enlarged left-brace 1st Row 1st column x + 3, 2nd column x less-than 0 2nd Row 1st column 3, 2nd column x greater-than-or-equal-to 0 EndLayout f(x) = StartLayout enlarged left-brace 1st Row 1st column negative x + 3, 2nd column x less-than-or-equal-to 0 2nd Row 1st column 3, 2nd column x greater-than 0 EndLayout f(x) = StartLayout enlarged left-brace 1st Row 1st column negative x minus 3, 2nd column x less-than-or-equal-to 0 2nd Row 1st column 3, 2nd column x greater-than 0 EndLayout

Answer 1

The graph corresponds to the function
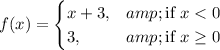`\(f(x) = \begin{cases} x + 3, & \text{if } x < 0 \\ 3, & \text{if } x \geq 0 \end{cases}\)`, featuring two connected lines with specific conditions for x. (option B)

The correct function represented by the graph is
`\( f(x) = \begin{cases} x + 3, & \text{if } x < 0 \\ 3, & \text{if } x \geq 0 \end{cases} \)`.

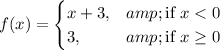The graph consists of two connected lines: the first line slopes upward from (-5, -2) to (0, 3), described by x + 3 for x < 0, and the second line continues horizontally at y = 3 for
`\(x \geq 0\)`.

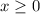This piecewise function captures the distinct behavior of the lines and correctly corresponds to the given graphical representation with specific conditions for x values less than 0 and greater than or equal to 0. (option B)

The complete question is:

The graph of a function is shown on a coordinate plane with two connecting lines. The first line goes from (-5, -2) to (0, 3), and the second line starts at (0, 3) and continues horizontally at y = 3. Which function is represented by the graph?

`A. \[ f(x) = \begin{cases} x - 3, & \text{if } x < 0 \\ 3, & \text{if } x \geq 0 \end{cases} \]\\\\\\\\B. f(x) = \begin{cases} x + 3, & \text{if } x < 0 \\ 3, & \text{if } x \geq 0 \end{cases} \]\\\\C. f(x) = \begin{cases} -x + 3, & \text{if } x \leq 0 \\ 3, & \text{if } x > 0 \end{cases} \]\\\\D. f(x) = \begin{cases} -x - 3, & \text{if } x \leq 0 \\ 3, & \text{if } x > 0 \end{cases} \]`