Question

What is the cell potential (emf, in V) of this cell at 25°C? Cu Cu2+ (0.0257 M) | Br2 [Br" (0.392 M) Answer:

Answer 1

Answer: The voltage of the cell is 0.80 V.

Step-by-step explanation:

The given cell is:

`Cu(s)/Cu^(2+)(0.0257M)||Br_2(l)/2Br^-(0.392M)`

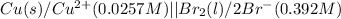
Half reactions for the given cell follows:

Oxidation half reaction:
`Cu(s)\rightarrow Cu^(2+)(0.0257M)+2e^-;E^o_(Cu^(2+)/Cu)=0.34V`

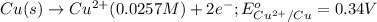
Reduction half reaction:
`Br_2(l)+2e^-\rightarrow 2Br^-(0.392M);E^o_(Br_2^/2Br-)=1.07V`

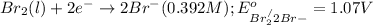
Net reaction:
`Cu(s)+Br_2(l)\rightarrow Cu^(2+)(0.0257M)+2Br^-(0.392M)`

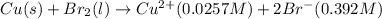
Oxidation reaction occurs at anode and reduction reaction occurs at cathode.

To calculate the
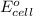`E^o_(cell)` of the reaction, we use the equation:

`E^o_(cell)=E^o_(cathode)-E^o_(anode)`

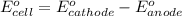
Putting values in above equation, we get:

`E^o_(cell)=1.07-(0.34)=0.73V`

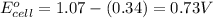
To calculate the EMF of the cell, we use the Nernst equation, which is:

`E_(cell)=E^o_(cell)-(0.059)/(n)\log ([Cu^(2+)]* [Br^(-)]^2)`

where,

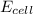`E_(cell)` = electrode potential of the cell = ?V

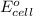`E^o_(cell)` = standard electrode potential of the cell = +0.73 V

n = number of electrons exchanged = 2

`[Cu^(2+)]=0.0257M`

`[Br^(-)]=0.392M`

Putting values in above equation, we get:

`E_(cell)=0.73-(0.059)/(2)* \log((0.0257)* (0.392)^2)\\\\E_(cell)=0.80V`

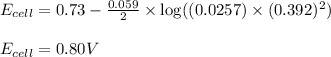
Hence, the voltage of the cell is 0.80 V.