Question

Q.2

The x coordinate of a point p is twice its y-coordinate. If p is equidistant
from Q (2,-5) and R (-3, 6) find the coordinates of p.
Q.3
Find the ratio in which y axis divides the line segment joining the points
A (5.-6) and B (-1,-4). Also find the coordinates of the point of division.
Q.4
Find the ratio in which the point(-3, k) divides the line segment joining
the points (-5,-4) and (-2,3). Also find the value of k.
Find the ratio in which pſ4, m) divides the line segment joining the
Q.5
pointsA (2,3) and B(6,-3)Hence find m.

Answer 1

Q2. (16,8)

Q3.
`k=(2)/(3)`, ratio=5:1

Q4. Ratio=2:1

Q5. Ratio=1:1

Explanation:

Q2. Let (2a,a) be the coordinates of P.

Since P is equidistant from Q (2,-5) and R (-3, 6), we have

`|PQ|=|PR|`

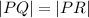
This gives us:

`√((2a-2)^2+(a+5)^2)=√((2a+3)^2+(6-a)^2)`

`\implies (2a-2)^2+(a+5)^2=(2a+3)^2+(6-a)^2`

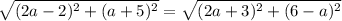
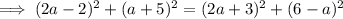
Expand:

`4a^2-8a+4+a^2+10a+25=4a^2+12a+9+a^2 -12a+36`

`2a=16`

`a=8`

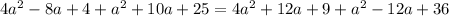
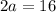
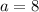
The coordinates of P are
`(16,8)`

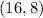
Q.3 The equation of the line segment joining the points

A (5.-6) and B (-1,-4) is
`x+3y=-13`.

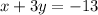The x-coordinate of the point that divides AB in the ratio m:n is

`x=(mx_2+nx_1)/(m+n)`

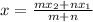
The y-axis meets this line at
`(0,-(13)/(3))`

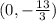
We substitute
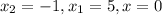`x_2=-1,x_1=5,x=0` into this equation and solve for m and n.

`0=(-m+5n)/(m+n)`

`m=5n`

`(m)/(n)=(5)/(1)`

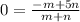
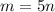
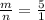
Therefore the ratio is m:n=5:1

Q.4 The equation of the line segment joining

the points (-5,-4) and (-2,3) is
`-7x+3y=23`.

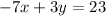The point (-3, k) must satisfy this line because it lies on it.

`-7(-3)+3k=23`.

`\implies k=(2)/(3)`

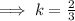
We again use the equation
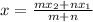`x=(mx_2+nx_1)/(m+n)` to find the given ratio.

Substitute:
`x_2=-2,x_1=-5`

`4=(-2m+-5n)/(m+n)`

`\implies m=2n`

`(m)/(n)= (2)/(1)`

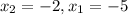
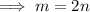
The ratio is m:n=2:1

Q. 5 The equation of the line joining A (2,3) and B(6,-3) is
`3x+2y=12`.

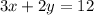We substitute (4,m) to get:

12+4m=12

4m=0

m=0

It is obvious that: (4,0) is the midpoint of A(2,3) and B(6,-3).

Hence the ratio is 1:1