Question

Determine if this is a linearly dependent or independent set: (V, V, V ) where syon V = (1,2,2,-1), V = (4,9,9,-4), v = (5,8,9,-5). Show all work and Explain your reasoning carefully

Answer 1

69

Explanation:

Answer 2

This is a linearly independent set.

Explanation:

We have these following vectors:

`V_(1) = (1,2,2,-1)`

`V_(2) = (4,9,9,-4)`

`V_(3) = (5,8,9,-5)`

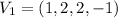
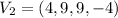
In a set of 3 vectors, if one of these vectors can be written as a linear combination of the 2 other vectors, they are linearly dependent. Otherwise, they are linearly independent.

We can verify this by solving the following system:

`xV_(1) + yV_(2) + zV_(3) = (0,0,0,0)`

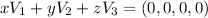
If the only solution is
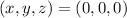`(x,y,z) = (0,0,0)`, they are L.I. Otherwise, they are L.D.

Solution:

`xV_(1) + yV_(2) + zV_(3) = (0,0,0,0)`

`x(1,2,2,-1) + y(4,9,9,-4) + z (5,8,9,-5) = (0,0,0,0)`

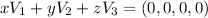
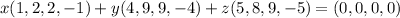
We have the following system of equations:

`x + 4y + 5z = 0`

`2x + 9y + 8z = 0`

`2x + 9y + 9z = 0`

`-x -4y - 5z = 0`

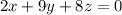
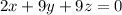
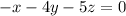
I am going to solve this by the row-reduction of the augmented matrix.

This system has the following augmented matrix:

`\left[\begin{array}{cccc}1&4&5&0\\2&9&8&0\\2&9&9&0\\-1&-4&-5&0\end{array}\right]`

To reduce the first row, i am going to make these following operations:

`L_(2) = L_(2) - 2L_(1)`

`L_(3) = L_(3) - 3L_(1)`

`L_(4) = L_(4) + L_(1)`

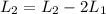
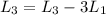
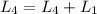
So the augmented matrix now is:

`\left[\begin{array}{cccc}1&4&5&0\\0&1&-2&0\\0&1&-1&0\\0&0&0&0\end{array}\right]`

Now I reduce the second row, doing:

`L_(3) = L_(3) - L_(2)`

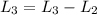
So the matrix is:

`\left[\begin{array}{cccc}1&4&5&0\\0&1&-2&0\\0&0&1&0\\0&0&0&0\end{array}\right]`

Now we can solve the system:

From the third line, we have that

`z = 0`

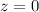
From the second line:

`y - 2z = 0`

`y - 2(0) = 0`

`y = 0`

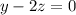
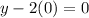
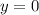
From the first line

`x + 4y + 5z = 0`

`x + 4(0) + 5(0) = 0`

`x = 0`

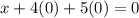
The only solution for this system is
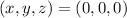`(x,y,z) = (0,0,0)`. This means that we have a linearly independent set.