Question

An urn contains 10 balls with the number ‘5’ printed on them, 6 balls with ‘4’ printed on them, and 4 balls with ‘2’ printed on them. Consider the experiment of picking a random ball from the urn and observing the number printed on the ball. If X is the number observed, what is E[X]?

Answer 1

Answer: 4.1

Explanation:

Given : An urn contains 10 balls with the number ‘5’ printed on them, 6 balls with ‘4’ printed on them, and 4 balls with ‘2’ printed on them.

Total balls = 10+6+4=20

Let A , B and C are the events of drawing ball with the number ‘5’, ball with the number ‘4’ and ball with the number ‘2’ respectively.

Then,

`P(A)=(10)/(20)=0.5\\\\ P(B)=(6)/(20)=0.3\\\\ P(C)=(4)/(20)=0.2`

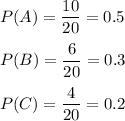
If X is the number observed.

Since
`E[X]=\sum_(i=1)^(n)x_ip_i`

Then,

`E[X]=5* P(A)+4* P(B)+2* P(C)\\\\=5* 0.5+4* 0.3+2* 0.2\\=4.1`

Hence, E[X]=4.1